Regressão Linear é uma das técnicas mais básicas em Machine Learning que podemos utilizar para realizar previsões. Neste artigo, quero te mostrar como a Regressão Linear se torna uma tarefa fácil quando trabalhamos com python.
Primeiro vou falar bem rápido sobre a Regressão Linear, se você ainda não sabe o que é, leia as próximas informações, mas se você está se sentindo seguro e quer partir direto pro código, vá direto para o Exemplo Prático!
O que é Regressão Linear?
A Regressão é uma técnica que tem por objetivo predizer o valor de uma variável dependente (Y) quando temos um conjunto de valores que são as variáveis independentes (X).
Para entender melhor esta definição, vamos imaginar que temos um conjunto de dados que tem uma tabela com duas colunas: A quantidade média de horas que um indivíduo passa em uma rede social e a sua quantidade de seguidores nesta rede social. Assim, nossa tabela é:
| ID | Horas | Nº Seguidores |
|---|---|---|
| 01 | 4 | 120 |
| 02 | 1 | 88 |
| 03 | 4.5 | 597 |
| 04 | 5.1 | 798 |
| 05 | 7 | 1500 |
Analisando a tabela acima, podemos perceber que existe uma tendência: Parece que quanto mais tempo o usuário passa nas redes sociais, mais seguidores ele possui.
Se existe uma relação entre a quantidade de horas que um indivíduo passa em uma rede social e a sua quantidade de seguidores, é possível prever a quantidade de seguidores de um usuário sabendo a quantidade de horas que ele passa nesta rede social?
Pronto! Chegamos onde queríamos: Na tarefa de Regressão.
Podemos considerar as horas passadas na rede social como X (variável independente) e a quantidade de seguidores como Y (variável dependente). Repare que nós estamos considerando que o número de seguidores depende da quantidade de horas que o usuário passa na rede social.
Agora que já definimos quem é X e quem é Y, devemos adotar um modelo de regressão para que seja possível prever a quantidade de seguidores de um individuo através da quantidade de tempo gasto na rede social.
Tipos de Regressão Linear
- Regressão Linear Simples: Na regressão linear simples, para cada valor de X (variável independente) temos apenas uma resposta Y (variável independente). Vamos ilustrar isto desta forma:
X -> Y
- Regressão Linear Múltipla: Nos deparamos com um problema de regressão linear múltipla quando temos um conjunto de valores X e para este conjunto tem-se apenas uma única resposta Y.
X1, X2, X3, ..., Xn -> Y
No caso do nosso exemplo, para cada valor de tempo que o usuário passa na rede social (X), temos uma única resposta, que é a quantidade de seguidores que ele possui (Y), portanto o nosso exemplo se trata de um caso de Regressão Linear Simples.
Exemplo Prático: Prevendo o custo de Seguro através da Idade do Paciente
O que você precisa para fazer este tutorial:
- Python 3.x;
- Pandas;
- Matplotlib
- Numpy;
- Um editor de código ou IDE de sua preferência.
- Faça download dos dados aqui
Mãos à obra ao código!
Primeiro precisamos importar os módulos necessários. Você pode copiar e colar o trecho de código abaixo:
1
2
3
4
5
6
7
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
from scipy.stats import pearsonr
Agora precisamos ler o arquivo que contém os dados.
1
dados=pd.read_csv('insurance.csv') #o meu arquivo com os dados está na mesma pasta que o arquivo do código
Conhecendo os dados
Primeiro precisamos conhecer nossos dados. Temos que saber do que se trata cada coluna e linha de nossa tabela que lemos do arquivo csv. Estes dados que estamos usando aqui foram disponibilizados pelo Kaggle neste link.
Vamos ver do que nosso dataset é composto:
1
2
3
#Verificando as primeiras 5 linhas do conjunto de dados
print(dados.head())
print(dados.shape)
O resultado mostrado no terminal será:
1
2
3
4
5
6
7
age sex bmi children smoker region charges
0 19 female 27.900 0 yes southwest 16884.92400
1 18 male 33.770 1 no southeast 1725.55230
2 28 male 33.000 3 no southeast 4449.46200
3 33 male 22.705 0 no northwest 21984.47061
4 32 male 28.880 0 no northwest 3866.85520
(1338, 7)
O comando print(dados.head()) nos mostrou as primeiras 5 linhas do nosso dataset, que possui 7 colunas. Já o comando print(dados.shape) nos revela que nosso dataset tem 1338 linhas e 7 colunas.
Em cada linha temos os dados de um paciente. Já para as colunas, temos as seguintes informações:
age: A idade do paciente
sex: O sexo do paciente
bmi: O índice de massa corporal (Body mass index) do paciente
children: Número de filhos que o paciente possui
smoker: Paciente fumante (yes) ou não fumante (no)
region: Região dos EUA na qual o paciente reside
charges: Valor financeiro cobrado pelo seguro individual de saúde.
Vamos ver também de qual tipo são os dados de cada coluna. Para isso basta adicionarmos a seguinte linha ao nosso código:
1
print(dados.dtypes)
Rode o código novamente e o resultado do comando acima será:
1
2
3
4
5
6
7
8
age int64
sex object
bmi float64
children int64
smoker object
region object
charges float64
dtype: object
Acabamos de ver que os dados das colunas que nos interessam (age e charges) são de tipos numéricos, portanto estão prontos para realizarmos as tarefas que queremos.
Antes de começar com a regressão linear, podemos plotar estes dados para termos certeza de que não estamos cometendo um erro ao associarmos a idade de um paciente com o custo do seu seguro de vida.
Vamos separar nossos dados definindo a variável independente (X) como a idade do paciente e o custo do seguro como a variável dependente (Y) e depois visualizar como é a relação entre estas variáveis. Para isso, utilizamos o seguinte trecho de código:
1
2
3
4
5
6
7
8
9
10
11
12
#Separando as variáveis X e Y
"""
Vamos modelar a relação entre o bmi e
o custo do seguro para clientes do sexo feminino e que sejam fumantes.
"""
dados = dados[dados['smoker'] == 'yes']
dados = dados[dados['sex'] == 'female']
X = dados['bmi'].values
Y = dados['charges'].values
Plotando o Gráfico de Dispersão e calculando o índice de correlação
Para ter uma ideia do comportamento dos nossos dados, precisamos plotar um gráfico de dispersão onde termos os valores de bmi no eixo x e os valores de custo no eixo y. Em python fazemos:
1
2
3
4
5
plt.scatter(X, Y)
plt.show()
r = pearsonr(X, Y)
print(f'Coeficiente de correlação: {r}')
Teremos o seguinte resultado:
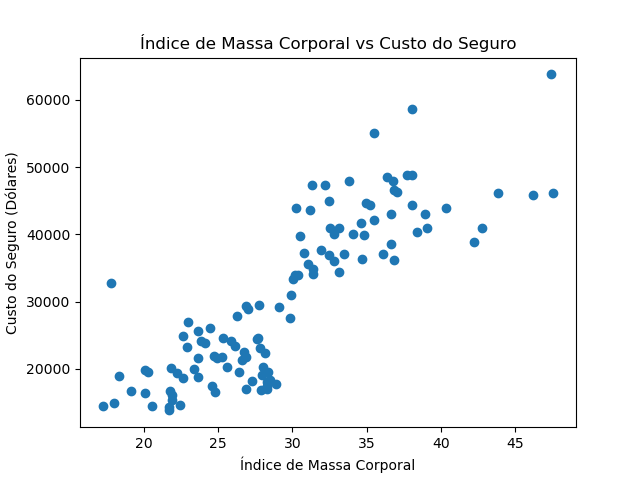
Quanto ao coeficiente de correlação temos:
1
Coeficiente de correlação: (0.8459098308542752, 1.2468184850708987e-32)
O primeiro valor é o coeficiente de correlação de Pearson, o segundo é o p-value. Podemos perceber que os dados estão correlacionados, uma vez que r é de aproximadamente 0.864 e o p-value é muito pequeno.
Assim, podemos agora partir para a modelagem.
Treinando o modelo
Precisamos dividir nossos dados em um conjunto de dados de treino (aqueles que usaremos para estimar os parâmetros do modelo) e de teste (que usaremos para avaliar o modelo estimado).
1
2
3
4
5
6
7
8
9
#Separando dados de treino e de teste
#utilizamos 70% dos dados para treino e o restante (30%) para teste.
x_train, x_test, y_train, y_test = train_test_split( X, Y, test_size=0.3)
#Precisamos redimensionar os dados para fazer a regressão linear
x_train=x_train.reshape(-1,1)
y_train=y_train.reshape(-1,1)
x_test=x_test.reshape(-1,1)
y_test=y_test.reshape(-1,1)
Agora podemos iniciar o treino:
1
2
3
4
#treinando o modelo
reg = LinearRegression()
reg.fit(x_train,y_train)
pred = reg.predict(x_test)
Vamos ver como nosso modelo se comporta e plotamos também o gráfico de dispersão do nosso dataset completo:
1
2
3
4
5
plt.scatter(X, Y, color="blue")
plt.plot(x_test, pred, color="red")
plt.title("Índice de Massa Corporal vs Custo do Seguro (Dados de Teste)")
plt.xlabel("Índice de Massa Corporal da Cliente")
plt.ylabel("Custo do Seguro (Dólares)")
O gráfico que obtemos é:
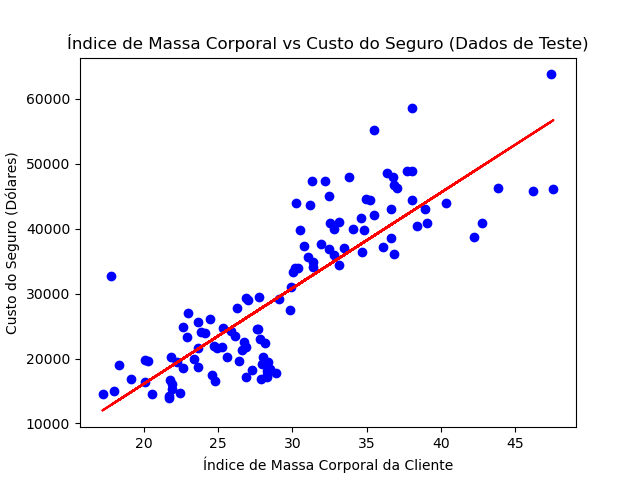
O modelo ajustado é representativo dos dados ou não?
Depois que fazemos a modelagem sempre nos perguntamos: E agora? Como saber se o que eu fiz é bom ou não?
Existem algumas métricas que podem nos ajudar a responder esta pergunta. Neste artigo vou falar apenas do coeficiente R-quadrado (r-squared) e dos resíduos, mas aconselho que você estude as demais métricas quando tiver a oportunidade.
1
2
3
4
5
6
7
8
9
10
r_squared = r2_score(y_test, pred)
print(f'Coeficiente r2: {r_squared}')
residual = y_test - pred
plt.title('Resíduos')
plt.xlabel('Resíduos (Dólar)')
plt.ylabel('Frequência Absoluta')
plt.hist(residual, rwidth=0.9)
plt.show()
Como resultado teremos:
1
Coeficiente r2: 0.5626850993817571
O que significa este valor? O r-quadrado é o coeficiente de determinação e ele expressa a porcentagem da variação da variável dependente que a variável independente explica corretamente.
Em outros paralavras, podemos dizer que o r-quadrado expressa o quanto o nosso modelo conseguiu explicar os dados. Seu valor varia entre 0 (o modelo não consegue explicar a relação entre as variáveis) até 100% (o modelo conseguiu explicar o relacionamento entre as variáveis).
O resultado que nós obtivemos foi de 56,27%, ou seja, nosso modelo conseguiu explicar a variação da variável independente em 56% dos casos.
Os resíduos
O histograma de frequência dos resíduos é:
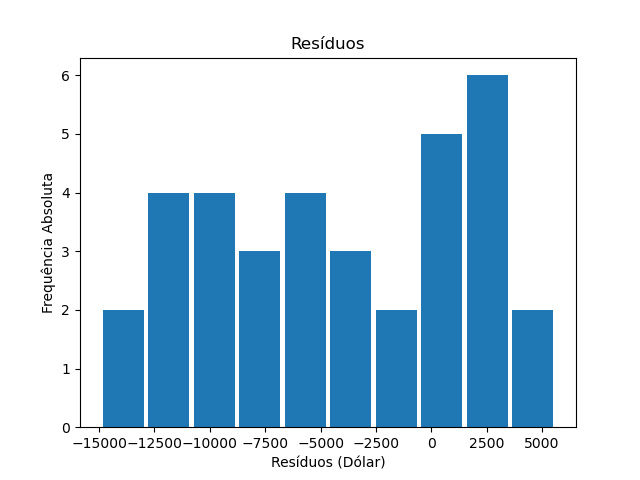
Os resíduos estão variando dentro de um intervalo de -15 mil dólares a 5 mil dólares. Isto está acontecendo pelo fato de termos muitos pontos que estão afastados da reta de regressão.
Desta forma, nós podemos perceber que nosso modelo não aproximou tão bem a realidade dos dados. Seriam necessárias outras análises para entendermos melhor o relacionamento entre os dados.
Mas acho que agora você já consegue treinar um modelo de regressão linear por conta própria, não é mesmo?
Se este artigo te ajudou, não deixe de compartilhar com seus amigos!