Muitos métodos estatísticos que utilizamos para análise de dados e tomada de decisões assumem que nossos dados seguem a distribuição normal.

Porém, é sempre bom fazer uma verificação desta suposição, uma vez que podemos realizar previsões que não se aproximam nem um pouco da realidade quando utilizamos métodos que assumem normalidade a dados que não “são normais”.

Este artigo se divide em duas partes: A primeira dá uma breve explicação sobre a distribuição normal e a segunda consiste em um exemplo prático de teste de normalidade de um conjunto de dados. Fique à vontade para ler o que lhe for mais conveniente.

O que é a Distribuição Normal?

Imagine que vamos coletar dados sobre o peso de recém-nascidos de uma cidade durante um certo período.

Quando nossa planilha tiver um número bem grande de recém-nascidos com seus respectivos pesos, poderemos plotar um histograma de frequências destes valores.

Vamos supor que plotamos o histograma de frequências e observamos um comportamento como este:

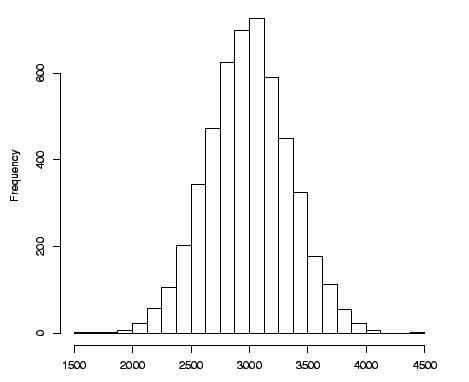Fonte: http://leg.ufpr.br/~shimakur/CE701/node36.html

Vamos interpretar algumas coisas sobre estes dados:

• Existe uma grande quantidade de recém-nascidos que têm peso próximo a 3000 g.

• A média dos pesos de recém-nascidos coincide (ou está muito próxima) com o peso da maioria dos recém-nascidos.

• A frequência de recém-nascidos com peso que se afastam do valor médio é menor quanto mais a seu peso se afasta da média.

Quando isso acontece, dizemos que temos um atributo (peso de um conjunto de recém-nascidos) que segue a Distribuição Normal.

Você, com certeza, já ouviu muito sobre a distribuição normal e deve estar se perguntando o motivo dela ser tão popular. A razão é simples: As medidas produzidas aleatoriamente em diversos processos seguem a distribuição normal.

Agora que você já tem uma noção preliminar do que é a distribuição normal, podemos defini-la de uma maneira mais formal:

“A distribuição normal de probabilidade é uma distribuição de probabilidade contínua que é simétrica em relação à média e mesocurtica e assíntota em relação ao eixo das abcissas em ambas as direções.” (CASTANHEIRA, 2012)

Com isso, nós podemos fazer uma afirmação:

• A probabilidade de ocorrência de indivíduos com alturas pesos próximos ao peso médio é maior do que os demais.

Exemplo Prático: Teste de Normalidade com Python

Em nossos projetos, podemos verificar se a distribuição dos dados com os quais trabalhamos é normal. Com python este processo é bem simples.

Mas primeiro, certifique-se de que você tenha os requisitos necessários para fazer este exemplo prático:

• Python 3.x
• Pandas, Numpy e Scipy

• Faça download dos dados aqui

• Lembre-se de descompactar os dados para fazer este exemplo prático!

Vamos supor que trabalhamos em uma companhia de seguros de vida e precisamos, por algum motivo, realizar alguns procedimentos utilizando este conjunto de dados. Estamos interessados em saber se a distribuição dos dados na coluna “bmi” é normal. Ou seja, queremos saber se o índice de massa corporal dos pacientes segue distribuição normal.

Para isso, vamos utilizar este algoritmo:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

dados = pd.read_csv('insurance.csv')

#Verificando as primeiras 5 linhas do conjunto de dados
print(dados.head())
print(dados.shape)

print(dados.dtypes)

plt.figure(figsize=(10,7), dpi= 80)
sns.distplot(dados['bmi'], color="dodgerblue", label="Compact",)

plt.show()

alpha = 0.05
k2, p = normaltest(dados['bmi'])

#Hipotese nula: Os dados seguem distribuição normal
#Hipotese alternativa: Os dados não seguem distribuição normal

if p < alpha:
    print("A Hipótese Nula pode ser rejeitada")
else:
    print("A hipótese nula não pode ser rejeitada")

Lendo o arquivo e conhecendo os dados

1
2
3
4
5
6
7

dados = pd.read_csv('insurance.csv')

#Verificando as primeiras 5 linhas do conjunto de dados
print(dados.head())
print(dados.shape)

print(dados.dtypes)

As primeiras linhas do código acima começam com alguns comandos que são muito úteis para conhecermos os dados.

Com o comando print(dados.head()) podemos visualizar as cinco primeiras linhas de cada coluna existente em nosso dataset. Este comando resulta na seguinte exibição no seu terminal:

1
2
3
4
5
6

   age     sex     bmi  children smoker     region      charges
0   19  female  27.900         0    yes  southwest  16884.92400
1   18    male  33.770         1     no  southeast   1725.55230
2   28    male  33.000         3     no  southeast   4449.46200
3   33    male  22.705         0     no  northwest  21984.47061
4   32    male  28.880         0     no  northwest   3866.85520

Os comandos print(dados.shape) e print(dados.dtypes) nos ajudam a verificar quantas linhas e colunas o dataset possui e também qual o tipo de dado armazenado em cada coluna. Se você observar no terminal, esses comandos resultaram em:

1
2
3
4
5
6
7
8
9

(1338, 7)
age           int64
sex          object
bmi         float64
children      int64
smoker       object
region       object
charges     float64
dtype: object

Com isso nós sabemos que o dataset tem 1338 linhas e 7 colunas. Cada linha representa um cliente e cada coluna tem uma informação sobre este cliente.

A coluna que nos interessa, “bmi” (índice de massa corporal), tem seus dados representados em float64.

Plotando o Histograma de Frequências

Neste trecho de código nós plotamos um histograma de frequências dos valores de bmi. Utilizamos a matplotlib e a seaborn para esta tarefa.

1
2
3
4

plt.figure(figsize=(10,7), dpi= 80)
sns.distplot(dados['bmi'], color="dodgerblue", label="Compact",)

plt.show()

E o resultado que obtivemos foi:

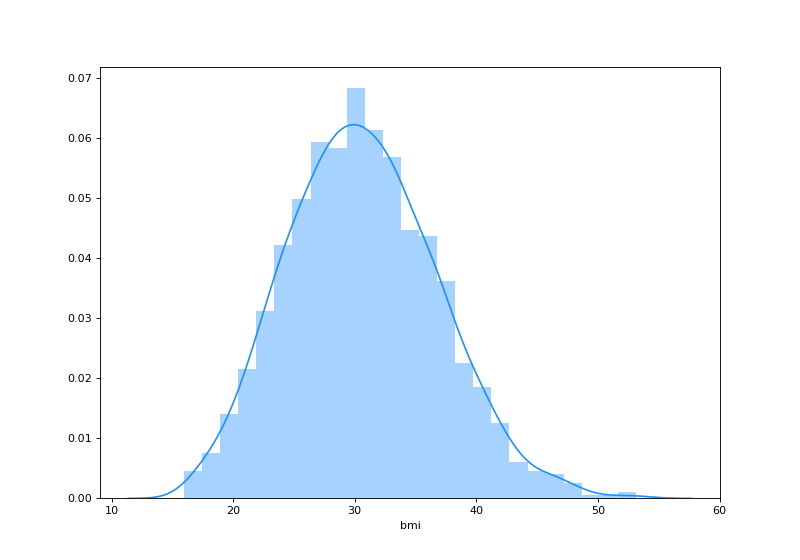
Olhando para esta figura, nós podemos pensar que os valores de índices de massa corporal dos clientes de nossa empresa de seguros seguem distribuição normal, porém, para validar esta afirmação, precisamos ainda realizar o teste de normalidade.

Fazendo o Teste de Normalidade

1
2
3
4
5
6
7
8
9
10

alpha = 0.05
k2, p = normaltest(dados['bmi'])

#Hipotese nula: Os dados seguem distribuição normal
#Hipotese alternativa: Os dados não seguem distribuição normal

if p < alpha:
    print("A Hipótese Nula pode ser rejeitada")
else:
    print("A hipótese nula não pode ser rejeitada")

E é aqui que acontece o que estávamos ansiosos para ver!

Utilizamos o comando normaltest(dados['bmi']) para verificar a normalidade da nossa amostra. Neste teste calculamos o p-valor e o k2. Além disso, definimos um valor alpha que serve como um threshold para rejeitar ou não a hipótese nula.

Vamos falar um pouco mais de cada um destes valores:

• p-valor: Pode também ser citado como valor-p. É a probabilidade de se obter um efeito tão extremo quanto o que está ocorrendo em nossos dados, assumindo que a hipótese nula é verdadeira. (Qual a probabilidade da distribuição que observamos naquele histograma ocorrer? Este é o p-valor).

• alpha: É o nível de significância, isto é, a probabilidade de rejeitarmos a hipótese nula quando ela é verdadeira. (Neste caso, a probabilidade de concluirmos que os dados não seguem a distribuição normal, quando na verdade seguem).

• k2: Este valor é, na verdade, a soma de dois termos elevados ao quadrado: s² + k². Sendo s o valor z obtido através do teste de assimetria (skewtest) e k é o valor da estatística z obtido pelo teste de curtose.

Rejeitamos a hipótese nula quando o valor-p for menor do que o nível de significância do nosso teste. Em outras palavras, estamos dizendo que se a probabilidade de ocorrência de valores como o que temos em nosso dataset (na coluna “bmi”) é maior do que a probabilidade de cometermos o erro de rejeitar a hipótese nula quando ela é verdadeira, podemos assumir que H0 é verdadeira. Este teste é conhecido como o Teste de Normalidade de Kolmogorov-Smirnov.

No caso do nosso conjunto de dados, podemos ver no terminal que o resultado foi:

1

A Hipótese Nula pode ser rejeitada

Ou seja, o valor-p foi menor do que nosso nível de significância, logo, a probabilidade de obtermos dados como estes é muito pequena. Assim, podemos concluir que os valores de índice de massa corporal dos clientes da empresa de seguros na qual trabalhamos não seguem distribuição normal.